top of page

ELECTROMAGNETISM
Magnetic Induction, Inductance, AC and LC Circuits
LC Circuit

LEARNING COMPETENCIES
-
Use analogies with the spring-mass system to draw conclusions about the properties of LC circuits.
-
Characterize the properties (stored energy and time-dependence of charges, currents, and voltages) of an LC circuit

REVIEW
What is an electric circuit?
An electric circuit is a path in which electrons from a voltage or current source flow. As stated on Simple Wikipedia, electrical current flow in a closed path is called an electic circuit.As shown on the image, a simple electric circuit is consists of voltage source (electron source), the path where the electrons will travel (black straight lines (wire)) and the lamp (load).

As this is a new lesson, you start doing the lecture by providing the basic concepts of LC circuit.
Consider the image on the right (inductor-capacitor circuit). You may notice that from the simple electrical circuit where there is a switch, voltage source and lamp as the load, the inductor-capacitor circuit now has added elements, namely: inductor and capacitor.
An electrical circuit consisting of an inductor, of inductance L, connected with a capacitor, of capacitance C is known as LC circuit.
The LC circuits we will be investigating are those involving a DC power supply. Let's begin with a simple circuit containing a DC power supply (battery), two switches, a resistor, a capacitor, and an inductor (refer to Image1 on the right for the inductor-capacitor circuit).
When only switch A is closed (both B switches are open), only the left circuit containing the resistor, battery, and capacitor is connected and the capacitor becomes charged. Once the capacitor is fully charged and has attained the voltage the battery, switch A is opened and both switch B's are closed. At that time only the capacitor and the inductor are components in the active circuit (refer to Image 1).
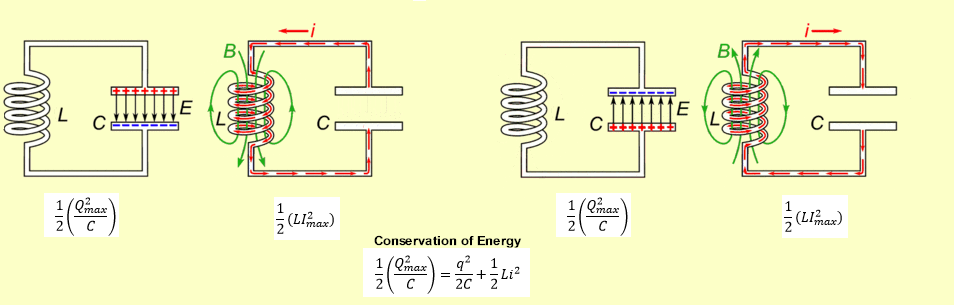
Initially the charges on the positive capacitor plate (we are discussing conventional current) will begin circulating counter-clockwise. As the current from the capacitor dies out, the inductor reverses its emf to keep the charges flowing until the bottom plate of the capacitor becomes positively charged and the top plate holds all of the negative charge. Then the process reverses and the current flows clockwise until the capacitor's top plate is once again positively charged and its bottom plate negatively charged. This process of "filling and emptying" the capacitor's plates, and its subsequent electric field, continues at a frequency (refer to Image 2).
Note that in the animation on Image2, the capacitor and inductor are presented on opposite sides compared to the introductory circuit presented on Image1.



The content being discussed is taken from physicslab.org.
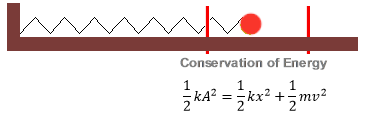
In a vibrating spring-mass system, the energy is shared between the elastic potential energy in the spring,
and the kinetic energy,
of the vibrating mass (refer to Image3).
At any intermediate position during a vibration, some of the energy is kinetic and some is potential elastic, but the total amount of energy remains constant (refer to Image4).
In an oscillating LC circuit, the energy is shared between the amount stored in the electric field of the capacitor and the amount storied in the magnetic field of the inductor (refer to Image5).
Here are the analogies that equate the behavior of an oscillating sping-mass system and resonating LC circuit:
-
mass becomes inductance, L
-
velocity becomes current, i
-
spring constant becomes C to the negative 1
-
displacement from equilibrium becomes charge, q
-
maximum displacement (amplitude) becomes Qo (the maximum charge on the capacitor)
Substituting our new variables into our equation for the energy of a vibrating mass-spring system, we get
But what is Qmax or Qo? This value comes from the functional equation for a capacitor: Q = CV where C is the capacitance and V is the voltage of the charging battery. When there is no charge on the capacitor (q = 0) we can calculate the maximum current.



BIG IDEA
LC Circuit can be Analogous to a Spring-mass systems

But what about the frequency of the circuit mentioned earlier? What would be its expression? Once again, we will turn to our analogies.
where the units of "LC" are sec2. The resonant frequency of the LC circuit is merely the reciprocal of its period,
In this presentation, the resistance in the circuit is considered minimal. That is, there are no energy losses to heat. In real circuits, the oscillations would eventually decay and die out.

ESSENTIAL QUESTION
What is an LC circuit?
An LC circuit is simply a closed loop with only two elements, a capacitor and an inductor. We will show that the LC circuits have resonant properties - they respond to certain frequencies. Therefore they can serve as the basis for any device that needs to tune to a specific frequency such as a radio. In an LC loop the charge oscillates back and forth through the capacitor with a given frequency just as a mass on a spring oscillates. To demonstrate this equivalence, we list several equations for both a mechanical spring and for an LC circuit.


BIG IDEA
LC Circuit is composed of Inductor and Capacitor
Simple electric circuit
Image1: Inductor-capacitor circuit
Image2: Tuned circuit. Image provided by Chetvorno via Wikimedia Commons.
Above image consists of an inductor L (coil of wire, left) and a capacitor C (right). E is the electric field (black arrows pointing up and down) and B is the magnetic field (in green).
Image3: spring-mass system
Image5: Oscillating LC circuit
Image4: spring-mass system after sometime
LC Circuit


LEARNING ALERT
Use pedagogical approach in delivering this content.
The parameters that determine the motion of a spring are the mass m, spring constant k, the position x, and the velocity v which is the rate of change of x. The parameters that determine the behavior of an LC circuit are L, C, Q and I which is the rate of change of Q. Thus there is a one-to-one correspondence since the equations of motion are identical given the substitutions.

bottom of page