top of page

Induced EMF

LEARNING COMPETENCIES

 

  • Calculate the induced emf in a closed loop due to time-varying magnetic flux using Faraday's law.

  • Compare and contrast electrostatic electric field and non-electrostatic /induced electric field.

BIG IDEA

Induced Electromotive Force (EMF) is equal to the rate of change of magnetic flux

Students are expected to already know what magnetic flux is, as well as the general equation for magnetic flux which is 

Prerequisite:

ESSENTIAL QUESTION

What does Faraday's equation mean?

Faraday's Law of EM induction is expressed in this equation:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

This formula tells us that the greater the number of loops the greater the induced voltage. The amount of magnetic flux that passes an area in a given time also matters that's why the relative speed of the magnet is also considered in the equation.The negative sign indicates that the induced voltage is in opposite direction of the magnetic field which will be explained further in Lenz's Law.

Concept Integration: At this point the teacher can now relate the "Let's Investigate activity or the Faraday's Experiment into the formula mentioned so students won't be overwhelmed since the equation is something that they have already undertood conceptually.

FORMATIVE ASSESSMENT

A rectangular coil of wire is situated in a constant magnetic field whose magnitude is 0.50 T. The coil has an area of 2.0 m2. Determine the magnetic flux for the three orientations, q  = 0˚, q  = 60˚, and q  = 90˚ (measured from a normal line drawn from the surface of the coil).   

    

ANSWER:  1.0 Wb, 0.50 Wb, and 0 Wb

Math Integration:

 Along with the introduction of the formula, the teacher can also integrate student's knowledge of basic calculus regarding the concept of derivative applied in the rate of change of magnetic flux.

Teacher can also review students' concept of the units such as Tesla (T) and Weber (Wb) and how they are connected to each other. Dimensional analysis of the units can also be shown so students can better understand and remember the formulas.

This shows the concept of magnetic flux that passes over a certain area. TutorVista (2015) NCS Pearson. Retrieved from
http://physics.tutorvista.com/electricity-and-magnetism/magnetism.html

MISCONCEPTION ALERT

Students need to be checked on their understanding of the magnetic flux passing a certain surface. Check whether they understood the significance of cosine theta in the equation. The teacher may ask about the amount of flux computed if the orientation of the surface is at 0 degrees or 90 degrees.

SAMPLE PROBLEM taken from Cutnell (2013)

A coil of wire consists of 20 turns, each with area of 1.5 x 10-3 m2. A magnetic field is perpendicular to the surface of each loop at all times, so that the initial orientation is at 0˚. At time t = 0, the magnitude of B at the location of the coil is 0.050 T. At a later time t = 0.10 s, the magnitude of the field at the coil has increased to 0.060 T.

a)     Find the average emf induced in the coil during this time.  

b)    What would be the value of the average induced emf if the magnitude of B decreased from 0.060 T to 0.050 T in 0.10 s?       

 

Suggestion to solve the problem:

1. Verify first what are the factors that we can assume as constant. In this case, the loop and the cross sectional area are constant. The only thing changing is the magnetic field with respect to time.

2. Apply the formula of Faraday's Law of Induction together with the concept of magnetic flux.

 

ANSWERS:    a.  -3.0 x 10-3 V

                       b. +3.0 x 10-3 V

Induced Electric Field vs Electrostatic Electric Field

BIG IDEA

Induced Electric Field is caused by changing Magnetic Flux in a Loop

 The image on the right shows the electric field lines of the positive (red) and negative (blue) charges at rest. This topic can be recalled first on how the field lines of positive and negative charge differ.

Wikimedia Foundation Inc ( 2015 October 24) Electric Field Retrieved from https://en.wikipedia.org/wiki/Electric_field

Review: The teacher can review on the electric field lines of stationary charges. He/She can ask students what happens to the field lines when charges are far from each other or near to each other. He/ She can also ask for the significance of field lines to the force experienced by charges

We were able to see from Faraday's experiment the time-varying magnetic field induced emf. Now, we are going to reinterpret Faraday's equation that is; a time-varying magnetic field can induce a non-conservative electric field in the coil.

 

 

 

 

 

The teacher can help the students understand the formula by reviewing the concept of line integral in their calculus

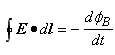
ESSENTIAL QUESTION

How does induced electric field behave?

         Consider the following illustration: A loop of wire with radius r is exposed to a time-varying magnetic field directed inside the coil. As the time varies, we can see how electric field E is induced around the loop that is directly tangent to the coil. The electric field produced is non-conservative in nature.

          If we consider a test charge q to be moved around the loop by the E field, we would find that work done is qε which is equal to qE(2πr) since the area is a circle.

A circular loop exposed to a constant magnetic field that is directed into the page. 

Kshitij Education India Private Limited (2015) Induced Emf and Electric Fields Retrieved from

http://www.kshitij-iitjee.com/induced-emf-and-induced-electric-field.

Using our previous knowledge on induced emf, we can change ε into the rate of change of magnetic flux: dϕB/dt

Applying the concept of line integral; ε can be expressed as the line integral of E over a closed path. Therefore, we can rewrite Faraday's Equation which is:

This is now the general equation of Faraday's Law.Note that E must be non-conservative field for it to be non-zero.

Note that ε represents emf or voltage while E represents Electric field. The teacher may use other notation such as V for emf to avoid confusion.

The following notations are also used in the equations:

r= radius

E=Electric Field

B=Magnetic Field

ΦB= Magnetic Flux

d/dt= change of something with respect to time (apply concept of derivative)

MISCONCEPTION ALERT

Teacher must take note whether the learners know the difference between conservative and non-conservative fields. The teacher can show illustration of its physical significance on the path dependence/non dependence to clarify the concept. Math lesson on line integral will be needed here.

bottom of page